Bought By: 12821
Rating: 4.8

Get Good Marks in your BCA Computer Application Programme in the Term-End Exams even if you are busy in your job or profession.
We've sold over 58,648,509 Help Books and Delivered 73,609,159 Assignments Since 2002.
As our customers will tell you...yes, it really result-oriented.




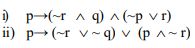 (c) Give geometric representation for followings:
i) {5, -3) x ( -2, -2)
ii) {-1, 3) x ( -2, 3)
Q2. (a) Draw Venn diagram to represent followings:
(c) Give geometric representation for followings:
i) {5, -3) x ( -2, -2)
ii) {-1, 3) x ( -2, 3)
Q2. (a) Draw Venn diagram to represent followings:
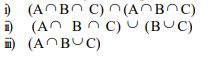 (b) Write down suitable mathematical statement that can be represented by the following symbolic properties.
(b) Write down suitable mathematical statement that can be represented by the following symbolic properties.
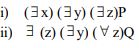 (c) Show whether √7 is rational or irrational.
Q3. (a) Explain use of inclusion-exclusion principle with example.
(b) Make logic circuit for the following Boolean expressions:
i) (xyz) + (xyz)' + (xz'y)
ii) ( x'yz) (xyz') (xy'z)
(b) What is a tautology? If P and Q are statements, show whether the statement
(𝑃 → 𝑄) ∨ ( →~ 𝑃) is a tautology or not.
Q4. (a) How many words can be formed using letter of “EXCELLENT” using each letter at most once?
i) If each letter must be used,
ii) If some or all the letters may be omitted.
(b) What is a relation? What are different types of relation? Explain equivalence relation with the help of example.
(c) Prove that
(c) Show whether √7 is rational or irrational.
Q3. (a) Explain use of inclusion-exclusion principle with example.
(b) Make logic circuit for the following Boolean expressions:
i) (xyz) + (xyz)' + (xz'y)
ii) ( x'yz) (xyz') (xy'z)
(b) What is a tautology? If P and Q are statements, show whether the statement
(𝑃 → 𝑄) ∨ ( →~ 𝑃) is a tautology or not.
Q4. (a) How many words can be formed using letter of “EXCELLENT” using each letter at most once?
i) If each letter must be used,
ii) If some or all the letters may be omitted.
(b) What is a relation? What are different types of relation? Explain equivalence relation with the help of example.
(c) Prove that To attend IGNOU MCS-13 Term-End Examination, you must first submit your Assignments to the university and it is possible from the MCS-13 study material. You can solve all necessary Assignments using Help Books. This will help in gaining good marks.
All best wishes with our efforts that you do not meet any obstacle before attending examinations next year. You can pass the BCA Computer Application Programme Annual Exams with a good grade using Books/Materials from any one place at home or anywhere else!
ALL THE BEST!!!
Team GullyBaba