Bought By: 11060
Rating: 4.6

Get Good Marks in your BSCG Mathematics Programme in the Term-End Exams even if you are busy in your job or profession.
We've sold over 44,941,341 Help Books and Delivered 55,312,769 Assignments Since 2002.
As our customers will tell you...yes, it really result-oriented.


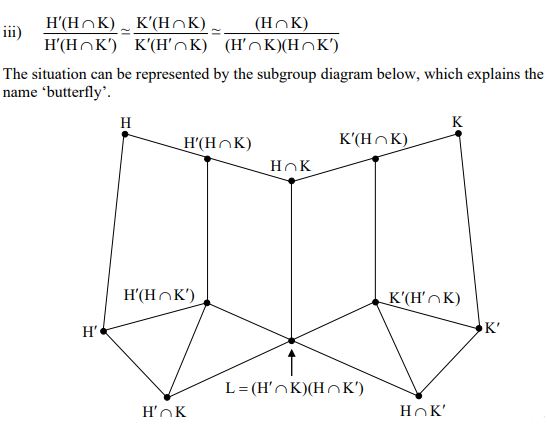




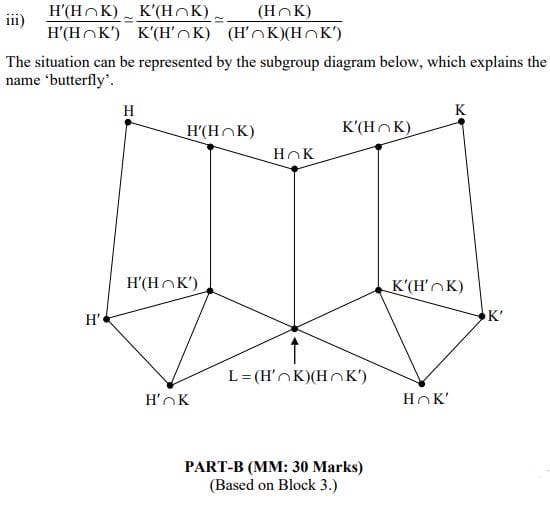


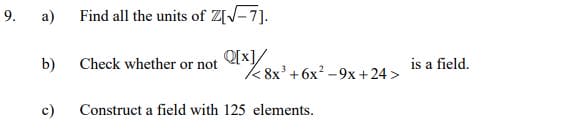
To attend IGNOU BMTC-134 Term-End Examination, you must first submit your Assignments to the university and it is possible from the BMTC-134 study material. You can solve all necessary Assignments using Help Books. This will help in gaining good marks.
All best wishes with our efforts that you do not meet any obstacle before attending examinations next year. You can pass the BSCG Mathematics Programme Annual Exams with a good grade using Books/Materials from any one place at home or anywhere else!
ALL THE BEST!!!
Team GullyBaba